Multi-digit division with area models and partial quotient is a major part of fourth grade standards. Confession: when I first moved to fourth grade, I had no clue how to divide with an area model or partial quotient! After teaching it to myself, I hated it! Dividing with area models and partial quotient didn’t click for me until I was actually teaching my class. All of a sudden, the pieces fell into place, and it all made sense. Hopefully, this post will save you the headaches I experienced.
One of the reasons dividing with area models and partial quotient was confusing for me is that I had not learned multi-digit multiplication or division conceptually. As a student, I only understood procedures. You can read more about the value of teaching both concepts and procedures here. In this post, I’ll keep the focus on multi-digit division.
For students to fully understand multi-digit division, they have to understand the concept of multiplication. If you want to see how I teach multi-digit multiplication, be sure to check out this blog post. It all ties together.
When teaching division with area models and partial quotient, we don’t want the strategies to be a series of steps for students to follow without any real meaning. We want students to grasp the how and why of what they are doing and to become flexible in their thinking. All of the division worksheets shown in this post are from my division unit. Even without the unit, you should be able to get a lot of good ideas for teaching dividing with area models and partial quotient.
Division Review
Before jumping in to multi-digit division, spend time connecting multiplication and division, as this well help students tremendously. You’ll also want to review the concept of division with a focus on interpreting the remainders. While students were taught these concepts in third grade, it’s one of those standards that will likely need significant review.
Multi Digit Division With Area Models
To be perfectly honest, I don’t love dividing with area models. In my eyes, it’s not an efficient way to divide. However, I do teach this, because of the foundation that it provides. I rarely have a student continue to use this method later in the division unit, but it still serves a valuable role. Students need to see the connections between multiplication, division, area models, and arrays. Once they put it together, this rest is much more natural for students.

In the division unit, there are plenty of guided practice opportunities and scaffolding for students.
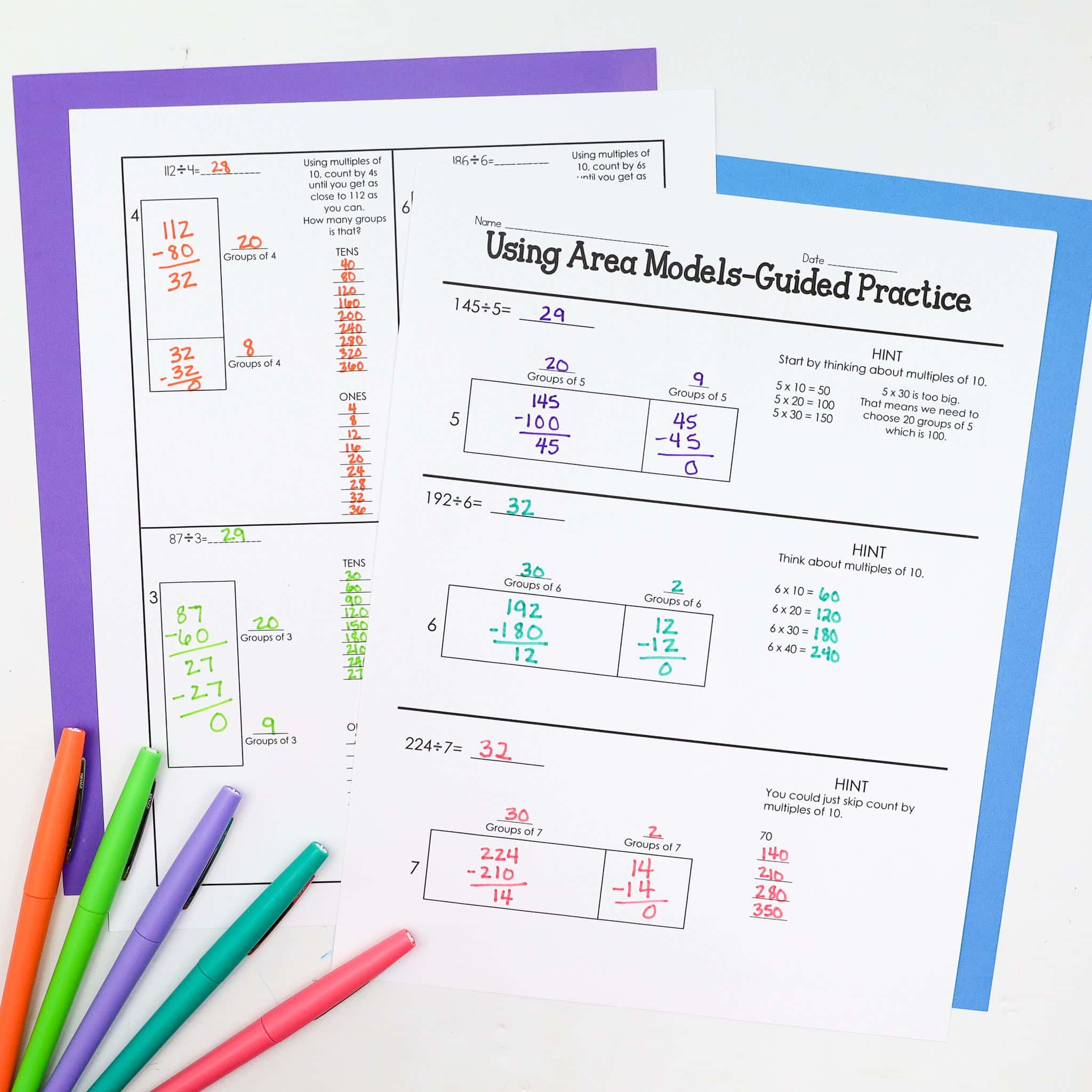
I also think it’s important to point out that I am not taking a formal assessment on division. This is a concept that students need ample time to learn before formally assessing.
Multi-Digit Division With Partial Quotient
Moving from division with area models to division with partial quotient typically an easy transition for students. They often wonder why I waited so long to show it to them! (I don’t introduce the algorithm at this point in the year, because I found that it confuses too many students.)

Since some students will need extra support, I included plenty of scaffolded, guided practice lessons.

Multi-Digit Division Problem Solving
The following lessons transition students to using partial quotient and then focus on problem solving. Once we reach this point in the unit, I let students use whichever strategy they prefer. The vast majority always chooses partial quotient.
It’s essential that students see the value and purpose in learning to divide. I always explain that in the real world, no one grows up to complete worksheets for a living. Instead, we use math to problem solve. I try to make these problem solving lessons meaningful and connected to my students’ lives.

Students always love this activity where they research different cars to find the best value for gas milage.

These problem solving lessons provide a great way to give students additional division practice in a meaningful way.
Division and Christmas
These lessons are in addition to my regular math lessons. It’s a fun, yet challenging, culminating project that incorporates multiplication and division.
In this activity, students are invited to enter a house in a holiday decorating contest. Students first select one of five different houses to decorate. They must determine how many feet of lights they need/want for their decorations. To calculate this, students measure the portions of their house they want to add lights. Students then purchase all of their decorating materials from The Exterior Illumination Specialist. 
All contestants (students) must submit a plan that accurately shows how their decoration budget is spent. They also create a plan for their design. The plan should show student measurements so confirm the exact length of lights needed. The plan must also show the desired location of each additional decorative feature.


All contestants must submit a final version of the decorated house. The house must be colored neatly with crayon. All decorations listed in the budget must be included in the final design. However, no additional lighting or decorations may be included.

You can find this Christmas Math Project here.
Multi-Digit Division Assessment
After a week of small group instruction, I am able to end the week with our division assessment. Once again, there are many options that you can use for your summative assessments.











