Developing Number Sense

Many upper elementary teachers notice a severe lack of number sense in their students, and that makes high levels of math extremely difficult for students. Number sense refers to “a well organized conceptual framework of number information that enables a person to understand numbers and number relationships and to solve mathematical problems that are not bound by traditional algorithms”. There are five components that characterize number sense: number meaning, number relationships, number magnitude, operations involving numbers, and referents for numbers and quantities. This post shares some strategies I use to develop number sense in upper elementary students. It’s certainly not too late to develop number sense with third, fourth, and fifth graders. Before we get started, I’d love to share a brief introduction to number sense video by Jo Boaler.

Hopefully, you’ll be able to use some of the ideas and strategies below to develop a number sense with your upper elementary students. More than likely, you’re already doing several of these things!

Browse the Number Sense Strategies:

1. Number Talks
2. Math Facts
3. Conceptual Instruction
4. Communication
5. Time

Number Sense Strategy 1: Number Talks

I heard about number talks several years before I ever tried implementing them. I convinced myself that they were a complete waste of my time and just another buzz word in education. However, I saw other math teachers that I greatly respected begin implementing number talks and sharing the success they were seeing. I was in fear of missing out, so I reluctantly gave number talks a try. To be honest, I did not have any positive expectations.

I am now happy to share that I was completely wrong! Number talks now have a valuable place in my classroom. My favorite number talks resource is Number Talks by Sherry Parrish. It is a long, content heavy book, but it’s not necessary to read cover to cover. I started by selecting the essential portions and teaching strategies as I learned them. One of my favorite things about number talks is that I don’t need any special resources or materials. I use the book for my lessons and my dry erase board. That’s it!

I quickly realized that number talks are an amazing routine that will help improve students’ number sense, and this is as important for upper elementary students as it is primary students. I’m sure we’ve all had students who have relied on rote algorithms to complete math problems, but these students did not understand what they are doing. We’ve all seen the same error patterns over and over again (forgetting to carry the one, subtracting from bottom to top, etc.) and these errors show how the lack of number sense impacts computation. When we develop number sense, students understand the underlying concepts of math operations.

When it’s time for our number talk, I have students sit on the carpet in front of my whiteboard. My rug isn’t quite large enough for my whole class, but we improvise the best we can. When students come to the rug, they don’t need to bring anything with them, since everything is done mentally. I use my Number Talks book to select 2-4 math problems for my students to solve for the day. I follow the order of suggested lessons in the book, but I’m sure you can skip around too! Next, I write one of the math problems on the board. I typically write the problem horizontally to discourage students from using the algorithm.

As students think about the problem, they hold their fist to their chest, and when they determine the solution, they replace their fist with a thumbs up. While students are waiting for the rest of the class to solve the problem, they should think of other strategies they could use and indicate the number of strategies they’ve though of by holding up two, three, or even four fingers to their chest. I like this procedure, because I can see who has solved the problem and who is thinking. It also prevents students from becoming intimidated by students who solve the problems quickly.

I ask students to share their answers, and I write all of the answers on the dry erase board. I then have students share how they solved the problem. As students explain their thinking, I write what they are telling me they did. After we go through the problem, students share if the strategy worked or not.

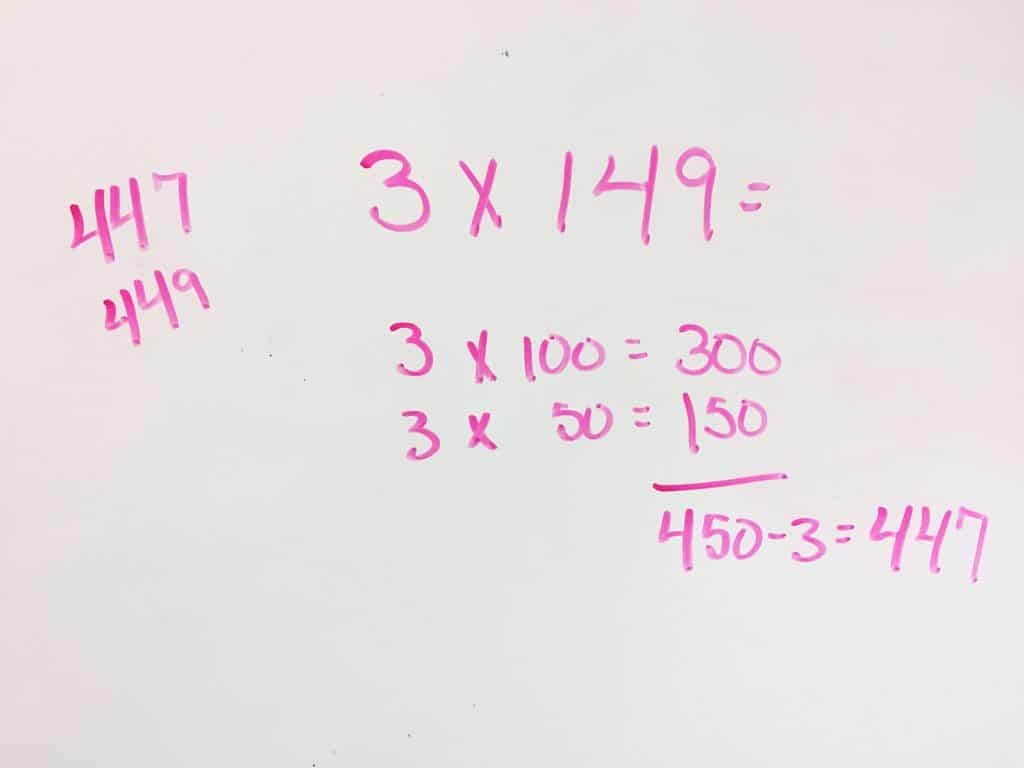
I explicitly teach the strategies from the Number Talk book before I expect students to apply that particular strategy, which is completely different from how I typically teach math. In a normal math lesson, I want students to construct their own rules and strategies, but this is a bit different. As I teach each strategy, I add them to our number talk anchor chart. The only bit of an issue that we ran into was that my students were coming up with too many different strategies. Our number talks could have gone on forever if I let them. However, I used this to guide discussions on the importance of selecting the most efficient strategy and how to determine which strategies were efficient.

To keep track of what problems I had used and who shared each day, I created forms for each strategy used for each operation. This is a great addition to a data notebook or teacher binder! You can download a free copy at the link below.

I can say with complete confidence that number talks are playing a significant role in improving my students’ number sense. They’ve also opened my eyes to why some students continue to make the same errors again and again and why some types of problems cause students so much difficulty. Even if you only have time for them two or three days a week, I strongly encourage everyone to at least give it a try!

Number Sense Strategy 2: Math Facts

As an upper elementary teacher I do focus on the memorization of math facts. I’ve found that higher levels of math are extremely difficult for students who do not know their basic math facts. However, I’m not a proponent of isolated memorization or high pressure timed tests either. Many of us have standards that include ‘fluency’ as a goal, and this fluency comes about when students develop number sense. But isolated practice and repetition will not develop number sense in our students.

Research tells us that the best mathematics classrooms are those in which students learn math facts through engaging activities that focus on mathematical understanding rather than rote memorization. When students focus on memorization, they often memorize facts without number sense. This means they are prone to making errors and are not flexible in their thinking. The best way to develop fluency with numbers is to develop number sense and to work with numbers in different ways, not to blindly memorize without number sense. There are three strategies I use to help students learn their math facts and develop number sense.

One strategy is through my Multiplication Fact Booklets. As students work through their booklets, they gain a conceptual understanding of each multiplication fact. They are able to solve the fact with multiple strategies, begin to observe patterns, and develop a mathematical vocabulary.

Another strategy I enjoy is incorporating meaningful multiplication games into my instruction. Games are effective and eliminate the high stress that timed tests bring to many students. Math games can be played for homework, morning work, math centers, or early finishers. I’ve created a set of Weekly Multiplication Games, and we focus on one game a week.

Xtra Math

When I first started teaching, I had a firm rule that for me to consider a student fluent with a math fact, s/he must be able to solve the math fact in 3 seconds or less. Over the years I’ve learned that some students will be slower when memorizing a fact or recalling a fact, but they still have exceptional math potential. I’ve shifted my mindset to allow for flexibility and reasoning in students’ thinking. I use Xtra Math as a multiplication fact practice tool, and I customize the program so my students have six seconds to solve a problem, rather than the defaulted three seconds. This gives my students the opportunity to apply multiplication strategies they’ve learned and builds math confidence with my students. Of course, if a student is sailing through without effort, I can adjust the time to 3 or even 1.5 seconds.

Flash Cards

I also like to put a spin on multiplication flash cards. With this twist, students match the cards with the same numerical answer. This activity encourages an understanding of multiplication as well as rehearsal of math facts. This is a great way to practice math facts while developing number sense. You can download a free set here.

Number Sense Strategy 3: Conceptual Instruction

To help our students continue to develop number sense and make sense of math, our math instruction must be conceptual, rather than a series of procedures. By far, the book with the biggest impact on my math lessons is Teaching Student-Centered Mathematics by John Van de Walle. The first time I read it, Van de Walle stepped all over my toes. I have many notes in the margins from the first time I read the book where I questioned everything I read. I’ve since reread the book several times, and acknowledge that I had a lot to learn when I first started teaching. I still do! This book challenges me to continually look at my math lessons and to find ways to improve those lessons.

When I started teaching, I often focued on algorithms, tricks, and shortcuts without first ensuring conceptual understanding. Algorithms and shortcuts are not necessarily bad. However, the key to using them correctly, lies in the sequence of events that occur in learning math concepts. Our math instruction must first ensure that students’ conceptual understanding is deeply embedded. When students have truly mastered a concept, and they should be able to show all the detailed steps in a process, explain why those steps occur. Once students reach this point, we can expose them to more efficient ways to express or perform those same processes. When we teach algorithms and shortcuts first, they become the means to get to the answer. When we bypass conceptual understanding, it is harder for students to understand more complex topics as they advance in school.

Over the years, I’ve modified my math instruction to allow students to construct their own understanding. For example, when using maipulatives, I no longer structure my lessons so that students are directed in exactly how to use the manipulatives. When I do this, my students are blindly following directions and look like they understand. But a rote procedure with a model is still a rote procedure. When getting answers rather than solving problems becomes the focus, students will gravitate to the easiest method available to get answers.

This does not help a student’s number sense, because the student is not reasoning with numbers. We must allow math to be problematic for students. A problem is a task where students have no prescribed or memorized rules or methods, nor is there a perception by students that there is a specific solution method. These problems focus students’ attention on ideas and sense making.

An example of a task that would be problematic for students is this divisibility task. In this assignment, students must add a digit to the ones place to create a number that is divisible by three, and students explain how they chose that number. Yes, I could simply have students memorize divisibility rules, but there is no application or problem in that lesson. We could make a cute craft or sing songs, but without authentically understanding the rule, students will not be able to apply what they have learned. Of course, I’m not criticizing crafts and songs! They’re a tool, but they are not enough for conceptual learning. You can download the divisibility task here.

Number Sense Strategy 4: Communication

My students ask me all the time why they have to write so much in math! Students should be able to think through what methods make sense and discuss the use of different methods. Communication of math ideas help students solidify their understanding of mathematics. Math can be thought of as a language, and communication plays an important role in making mathematics meaningful.

I occasionally have students write about math through Math Journal Prompts. I had my prompts for the year bound into books for my students, and they regularly write in their journals. The prompts are not word problems or multi part problems. They’re unique in the sense that they’re opened ended and encourage metacognition and evaluation.

I also try to regularly incorporate writing in my math tasks. I have students explain how they solved the problem using multiple representations. Getting a good response is typically like pulling teeth at the beginning of the school year. But with extensive modeling and practice, students always come around.

Number Sense Strategy 5: Time

I was hesitant to add time to this post, because it’s something we don’t have a lot of control over as teachers. As I write this, I recognize that I’m preaching to the choir. I get it. I’m teaching full time, so I’m right there with you. However, it’s hard to mention the topics above without at least mentioning time. We all know that there isn’t enough time in the day to do all that we need to do, and there isn’t enough time in the school year to effectively teach all of our standards.

One thing we have to look at is our daily schedule. I’ve heard of classrooms with math blocks of 25 and 30 minutes. With that short of time frame, there is no way to adequately teach math standards and build number sense. Many of us have no control over the time allotted for each subject, but if possible, I recommend at least an hour a day for math. With our daily time crunch, it’s important to eliminate as much down time and transition time as possible.

Every year I feel I have to move so fast through math standards that my students don’t have time to truly understand and conceptualize the standards. Conceptual instruction takes longer than procedural instruction, so I’m not able to rapidly move through the standards. This leaves me in a panic after Christmas, because I have little time left to teach so many things. I’m learning to spend the bulk of my time on my essential standards or power standards. Those are the standards that it’s important for students to master for success in math in later years. For me, those are my place value, addition, subtraction, multiplication, division, fraction, and decimal standards. I absolutely teach my other standards, but I don’t go as deep as I would like because of time constraints.

In my experience, math is a subject that is often short changed. Whether it’s professional development, early intervention programs, RTI, or after school tutoring, there always seems to be less of an emphasis on math. I teach reading too, so I’m completely on board with supporting students as much as possible with reading, but I don’t think math should be neglected either.

I’m learning, not there yet, to not waste my energy complaining or worrying about what I can’t control. I’ll continue to advocate for high quality math instruction, but if I only focus on what’s wrong, I won’t make positive gains. I tutor one afternoon a week after school, because I know it’s a need for my students. A coworker and I have set aside time for biweekly professional development, because we’re not satisfied with where we are in our instruction. We want to continually improve. These are things I can do something about, and the rest….well, maybe one day.

I’ve found that the best way to instill number sense is through my math warm-ups. This incorporates each of these strategies, using only about 10 minutes a day-at most! If you’d like to learn more about my warm-ups, be sure to check this out. I also have a post with more information on math warm-ups.